Zabezpieczenie belki stalowej przed zwichrzeniem

Współpraca belki stalowej z blachą trapezową, płytą warstwową lub żelbetową

1. Informacje wstępne

Połączenie belki stalowej z konstrukcyjnym elementem powierzchniowym może zapewnić jej dodatkowe podparcie ciągłe, a tym samym zabezpieczyć całkowicie lub częściowo przed utratą płaskiej postaci zginania, czyli przed zwichrzeniem.

Stężenie ciągłe belki stalowej w myśl normy PN-EN 1993-1-1 załącznik BB (dalej [N1]) realizowane jest jako:
  1. ciągłe stężenie boczne wynikające ze sztywności postaciowej współpracującego elementu powierzchniowego S, 
  2. ciągłe stężenie przeciwskrętne wynikające ze sztywności obrotowej współpracującego elementu powierzchniowego Cϑ,k. 

2. Boczne stężenie ciągłe w rzeczywistej konstrukcji 

Boczne podparcie ciągłe elementu belkowego może być realizowane m.in. przez:
  1. płytę żelbetową (por. Rys. 1a), 
  2. blachę trapezową (por. Rys. 1b) 
  3. płytę warstwową (por. Rys. 1c). 

a)  

b)  
c) 

Rys. 1. Elementy konstrukcyjne pozwalające na realizację bocznego podparcia ciągłego: 
a) płyta żelbetowa, b) blacha trapezowa, c) dachowa płyta warstwowa 

We wszystkich wymienionych przypadkach elementy konstrukcyjne (płyty) wraz z analizowanym elementem belkowym mogą tworzyć tak zwane przepony (tarcze). Ich sztywność postaciowa S i obrotowa Cϑ,k uzależniona jest od szeregu aspektów, które poruszone zostaną w kolejnych częściach tego tematu. Aby wymienione elementy konstrukcyjne zapewniały stężenie boczne i przeciwskrętne muszą być odpowiednio połączone ze stężanym elementem (belką). W przypadku płyty żelbetowej mowa jest o bezpośrednim (Rys. 2a) lub pośrednim (Rys. 2b) połączeniu pasa ściskanego belki z płytą żelbetową. 

a)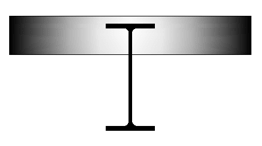 

b)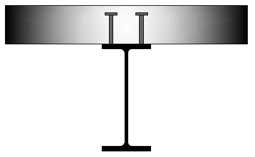 

Rys. 2. Połączenie płyty żelbetowej z belką stalową: a) bezpośrednie, b) pośrednie 

W przypadku blachy trapezowej/płyty warstwowej stężenie uzyskujemy poprzez bezpośrednie mocowanie blachy trapezowej/płyty warstwowej do belki za pomocą wkrętów samowiercących. 

a) 
b) 

Rys. 3. Wkręt samowiercący stosowany przy mocowaniu do elementów stalowych: 
a) blachy trapezowej, b) płyty warstwowej 

3. Pełna stabilizacji belki

Zgodnie z [N1] pełna stabilizacja belki stalowej (brak zwichrzenia) będzie zapewniona wtedy, gdy spełnione zostanie kryterium (BB.2) [N1] sztywności postaciowej oraz kryterium (BB.3) [N1] sztywności obrotowej.

3.1. Kryterium sztywności postaciowej S ≥ Sb


(W.1)  
gdzie: 
S – sztywność postaciowa (na jednostkę długości belki), która zależy od rodzaju elementu powierzchniowego - omówione w kolejnych częściach,
E – moduł Younga,
G – moduł Kirchhoffa,
Iw – moment bezwładności przy skręcaniu skrępowanym (wycinkowy),
It – moment bezwładności przy skręcaniu swobodnym (St. Venanta),
Iz – moment bezwładności przekroju względem osi z-z,
L – długość belki,
h – wysokość belki. 

3.2. Kryterium sztywności obrotowej Cϑ,k≥ Cb


(W.2)
gdzie:
Cϑ,k – sztywność obrotowa (na jednostkę długości belki) związana z rodzajem elementu powierzchniowego i jego sposobem połączenia z belką,
Mpl,k – wartość charakterystyczna nośności plastycznej przekroju belki przy zginaniu,
Kυ – parametr zależny od rodzaju analizy: 
0,35 w przypadku analizy sprężystej, 
1,0 w przypadku analizy plastycznej,
Kϑ – współczynnik uwzględniający rozkład momentów i warunki zamocowania (Tablica BB.1 w [N1]).

3.3. Wytyczne do stosowania przy analizie bocznego podparcia ciągłego

W przypadku belki stalowej połączonej z płytą żelbetową (belka zespolona) informacje dotyczące zabezpieczenia jej przed zwichrzeniem znajdują się w pkt. 6.4 normy PN-EN 1994-1-1 Projektowanie zespolonych konstrukcji stalowo-betonowych (dalej [N6]). Zgodnie z tym punktem normy za belkę zabezpieczoną przed zwichrzeniem uznajemy taką belkę, której półka ściskana połączona jest z płytą żelbetową (przykładem takim jest belka swobodnie podparta której ściskana półka usztywniona jest płytą żelbetową). W przypadku belek, których półki ściskane nie są usztywnione płytą żelbetową (np. belki ciągłe) oznacza to konieczność sprawdzania możliwości ich zwichrzenia.

Z kolei dla połączenia blachy trapezowej lub płyty warstwowej z belką istnieją wytyczne normowe i literaturowe, których zakres jest ograniczony i niejednoznaczny.
Kwestie stężenia belki blachą trapezową zostały omówione w p.10.1 normy PN-EN 1993-1-3:2008 (dalej [N2]). Są one również przedmiotem wytycznych ECCS No88 European Recommendations for the Application of Metal Sheeting acting as a Diaphragm (dalej [2]). 

Wspomniana norma [N2] ogranicza zakres opisanej procedury stężenia do elementów (określone są one jako płatwie) zimnogiętych o przekroju Z, C, ∑, U i kapeluszowym - p.10.1.1 (1). Rozszerzenie zakresu stosowania wspomnianej procedury (ale w odniesieniu do innych kształtowników i blach profilowanych na zimno) możliwe jest po przeprowadzeniu badań zgodnie z Załącznikiem A wspominanej normy.
Niespójnością jest zatem powoływanie się normy [N1] w załączniku BB.2 na zapisy normy [N2], gdyż norma [N1] po pierwsze ogranicza się do elementów o grubości ścianki t ≥3,0mm, a po drugie dotyczy wymiarowania elementów gorącowalcowanych. Z kolei dokument źródłowy [2] nie wprowadza ograniczenia opisanego w p.10.1.1(1) normy [N2].

Warto w tym miejscu wspomnieć, że norma [N2] w punkcie 2 (6) wprowadza KLASY KONSTRUKCJI, które definiują rolę elementów zimnogiętych i blachy trapezowej w stateczności globalnej obiektu: 
  1. Klasa konstrukcyjna 1 – konstrukcja, którą projektuje się z uwzględnieniem udziału kształtowników i blach profilowanych na zimno w nośności i stateczności całego układu,
  2. Klasa konstrukcyjna 2 – konstrukcja, którą projektuje się z uwzględnieniem udziału kształtowników i blach profilowanych na zimno w nośności i stateczności pojedynczych elementów,
  3. Klasa konstrukcyjna 3 – konstrukcja, w której blacha trapezowa profilowana na zimno tylko przenosi obciążenia na konstrukcję.

Informacje, które będą dalej poruszane odnoszą się do konstrukcji w klasie 2.

Należy też pamiętać, że nałożenie na blachę trapezową zadania konstrukcyjnego pociąga za sobą konieczność właściwego jej połączenia z usztywnianym elementem na poziomie projektowania i wykonawstwa ([1]). Jakość wykonania połączenia podlega wtedy kontroli i odbiorowi technicznemu zgodnie z normą  PN-EN 1090-4:2018 "Wykonanie konstrukcji stalowych i aluminiowych Część 4: Wymagania techniczne dotyczące profilowanych na zimno stalowych elementów konstrukcyjnych oraz konstrukcji poszycia dachów, sufitów, stropów i ścian" (dalej [N3])
Można również rozważyć zamieszczenie tablic informacyjnych na obiektach zakazujących modernizacji poszycia (np. montaż dodatkowych świetlików, wykonywanie otworów wentylacyjnych itp.) bez wcześniejszych obliczeń statyczno-wytrzymałościowych. 

W przypadku płyty warstwowej aspekt stężenia belek jest przedmiotem intensywnych badań naukowych. Na dzień dzisiejszy wyniki prowadzonych badań zostały zestawione w CIB Publication 379 European Recommendations on the Stabilization of Steel Structures by Sandwich Panels (dalej [3]) 
W przygotowaniu (stan na 09.2020) jest również norma prEN 14509-2:2016 Double skin metal faced insulating panels. Factory made products. Specifications. Part 2: Structural applications - fixings and potential uses of stabilization of individual structural elements (dalej [N4]).

4. Definicja bocznych podpór ciągłych w AxisVM

Spełnienie kryteriów pełnej stabilizacji podanych w poprzedniej części powoduje, że możemy pominąć weryfikację elementu stalowego na zwichrzenie. Wówczas w AxisVM w parametrach do wymiarowania elementu stalowego wystarczy odznaczyć Zwichrzenie.


Rys. 4. Wyłączenie zwichrzenia dla weryfikowanego elementu stalowego.

W większości sytuacji projektowych występuje jednak tylko częściowe zabezpieczenie przed zwichrzeniem, co pociąga za sobą konieczność wyznaczenia sprężystego momentu krytycznego Mcr. W programie AxisVM wyznaczenie tej wartości może zostać przeprowadzone:
  1. na podstawie ogólnego wzoru (W.3) przytoczonego w prenormie ENV 1993-1-1:1992 załącznik F (F.2) (dalej [N5])
  2. lub za pomocą wbudowanego w AxisVM narzędzia AutoMcr

4.1. Ogólny wzór na Mcr


(W.3)
gdzie:
E - moduł sprężystości podłużnej (E = 210000 N/mm2),
G - moduł sprężystości poprzecznej (G = 80770 N/mm2) 
Iz - moment bezwładności względem osi słabszej,
It - moment bezwładności przy skręcaniu swobodnym,
Iw - wycinkowy moment bezwładności,
L - odległość między punktami bocznego podparcia,
k oraz kw - współczynniki długości efektywnej,
zg - odległość od punktu przyłożenia obciążenia do środka ścinania przekroju,
zj – miarodajny dystans dla uwzględnienia asymetrii względem osi y-y. 

zs - współrzędna środka ścinania
C1 – jest współczynnikiem zależnym od kształtu wykresu momentu zginającego pomiędzy stężeniami bocznymi,
C2 – jest współczynnikiem zależnym od punktu przyłożenia obciążenia względem środka ścinania przekroju poprzecznego belki,
C3 – jest współczynnikiem korygującym ze względu na asymetrię przekroju względem osi y-y. 

Korzystanie ze wzoru (W.3) jest uzasadnione przy typowych sytuacjach projektowych, gdy element belkowy jest bocznie podparty punktowo. Mimo dość rozbudowanej postaci i wielu zmiennych, to dla elementu bisymetrycznego projektant podaje w programie jedynie wartość kw oraz ewentualnie C2. Do wad tego rozwiązania należy zaliczyć fakt, że wartość k jest definiowana na poziomie parametrów wyboczenia giętnego, a to oznacza, że przyjmowana długość efektywna musi być taka sama dla wyboczenia giętnego jak i giętno-skrętnego (zwichrzenia). Ponadto wzór ten traci swoje zastosowanie przy odcinkowych podporach ciągłych. 

4.2. AutoMcr, czyli dyskretna analiza zwichrzenia

Znacznie szersze zastosowanie praktyczne ma AutoMcr, które na podstawie zdefiniowanych jedynie charakterystyk podpór jest w stanie automatycznie wykonać analizę zwichrzeniową wyodrębnionego elementu stalowego. Podparcia mogą zostać zdefiniowane w dowolnych miejscach na długości elementu, a współczynniki wyboczenia giętnego nie wpływają na przeprowadzaną analizę zwichrzenia. Zaimplementowana analiza opiera się na tym samym podejściu, co w popularnym, uznawanym za referencyjny w tej kwestii, programie LTBeam.

Definicję dodatkowych podparć bocznych warto rozpocząć z podporami wstępnie pobranymi z modelu globalnego (zaznaczona opcja Zwichrzenie / Podpory boczne / Automatyczna w oknie Parametry wymiarowania - rys. 5), a następnie kliknąć w przycisk [...] w celu dalszego ich dodawania/modyfikowania.


Rys. 5. Przycisk otwierający okno do definicji podparć bocznych w metodzie AutoMcr

Poniższy rysunek pokazuje sposób definicji parametrów podpory ciągłej. 

Rys. 6. Wywołanie okna do definicji ciągłej podpory bocznej

Definicja ciągłego podparcia bocznego odbywa się na trzech poziomach:
  1. Zdefiniowanie odcinka na którym podparcie boczne jest realizowane (Położenie),
  2. Określenie mimośrodu podparcia względem wysokości przekroju (Mimośród),
  3. Określenie sztywności podparcia (Sztywność) definiowanego przez trzy składowe w układzie lokalnym belki:
  4. Ry - odpowiada za ruch translacyjny elementu po kierunku osi -y- 
  5. Rxx - odpowiada za obrót elementu wokół osi podłużnej -x-
  6. Rzz - odpowiada za obrót elementu wokół osi -z- przekroju.

Korzystając z tej funkcji należy pamiętać, że odcinek zamieniany jest na n podpór punktowych na metr długości elementu (sugerowana minimalna liczba podpór na metr wynosi 4). Definiując sztywności podparcia wprowadzamy wartość sztywności na metr długości elementu. Sztywność ta przypisywana jest podparciom pośrednim, a podparcia skrajne przyjmują połowę zdefiniowanej wartości sztywności. Na przykład deklarując Ry = 1000 kN/m/m dla n = 4 program przypisze sztywność podparć pośrednich równą 250 kN/m, a skrajnych 125 kN/m.

5. Blacha trapezowa jako stężenie belki

5.1. Wymagania dla blachy trapezowej stężającej elementy prętowe

Wykorzystanie blachy trapezowej do przeniesienia ścinania w płaszczyźnie pokrycia nakłada na projektanta konieczność sprawdzenie warunków wykraczających poza warunki związane z podstawową funkcją blachy trapezowej tj. przeniesienie obciążeń zewnętrznych na elementy ją podpierające. Wiąże się to przede wszystkim z oceną możliwości zniszczenia wynikającego z jej pracy tarczowej. Poniżej wymieniono mechanizmy zniszczenia które należy uwzględnić w przypadku rozpatrywania blachy trapezowej jako przepony: 
  1. miejscowa utrata stateczności płaskich ścianek pod różnym obciążeniem; 
  2. nośność blachy trapezowej wynikająca z jej zginania, ścinania, rozciągania lub ściskania;
  3. wyboczenie elementów obrzeżających przeponę lub zniszczenie łączników należących do tych elementów; 
  4. ogólna utrata stateczności ścinanej przepony; 
  5. zniszczenie łączników przy rozpatrywaniu różnych ich postaci.

Szczegółowe procedury określające metodologię określania wyżej wymienionych mechanizmów zniszczenia znajdują się w [6] oraz [2].
Poniżej przedstawiono tok obliczeń w kontekście wymiarowania belki stalowej stężonej przez blachę trapezową w oparciu o wytyczne normy [N1] oraz [N2] przy założeniu spełnienia wspomnianych warunków pracy tarczowej przez blachę i jej łączniki.

5.2. Sztywność blachy trapezowej

W przypadku blachy trapezowej, zgodnie z normą [N1] załącznik BB.2 i normą [N2] p.10.1 określa się:
  1. sztywność postaciową S do wyznaczenia sztywności ciągłego stężenia bocznego (zabezpieczenie przed wyboczeniem),
  2. sztywność obrotową Cϑ,k do wyznaczania sztywności ciągłego stężenia przeciwskrętnego (podparcie ze względu na obrót).
Sztywność postaciowa S
Sztywność ta (por. Kryterium sztywności postaciowej) dla poszycia wykonanego z blachy trapezowej połączonej ze ściskanym pasem belki w dolinie każdej fałdy (łączniki główne) po obu stronach zakładki i na obrzeżu (łączniki wzdłużne) określona jest w jednostkach N wg [N2] wzorem 10.1b:


(W.4)

gdzie
t – grubość blachy trapezowej [mm]
broof – szerokość dachu [mm]
s – rozstaw między belkami [mm]
hw – wysokość blachy trapezowej [mm]

W przypadku innych warunków łączenia belki z blachą trapezową, wyznaczenie sztywności S musi być wyznaczone indywidualnie, zgodnie z wytycznymi podanymi w [2].

Interpretacja parametru broof.
Określenie „szerokość dachu” przytoczone w normie wydaje się być niejednoznaczne i mało precyzyjne. W praktyce projektowej możemy mieć do czynienia z dachem płatwiowym lub bezpłatwiowym. Wymiar broof zgodnie z dokumentem [2] należy rozumieć jako wymiar równoległy do rozpiętości blachy trapezowej. Poniżej przedstawiono ten parametr na rysunkach, w celu łatwiejszej interpretacji.


Rys. 7. Wymiar b_roof dla dachu płatwiowego


Rys. 8. Wymiar b_roof dla dachu bezpłatwiowego

5.3. Weryfikacja kryterium sztywności postaciowej dla blachy trapezowej

S ≥ Sb
Jeżeli spełniony jest warunek (W.1) Kryterium sztywności postaciowej, wtedy uznajemy, że przy definiowaniu podpór bocznych do analizy zwichrzenia w AutoMcr możemy przyjąć podpory niepodatne (wartość sztywności Ry = 1*E10 [kN/m/m]).

S < Sb
Dla takiego rezultatu norma określa tylko, że analizowany element belkowy nie jest stężony poprzecznie na swojej długości. Dysponując jednak odpowiednimi narzędziami obliczeniowymi, możliwe jest wykorzystanie podparcia z blachy trapezowej do częściowej stabilizacji belki zginanej. Mamy wtedy do czynienia z tzw. stabilizacją sprężystą, gdzie wartość sztywności podparcia bocznego Ry można łatwo wyznaczyć na podstawie sztywności postaciowej S blachy trapezowej ze wzoru
Ry = S / L1 
(W.5)
gdzie
L1 jest odcinkiem, na którym realizuje się podparcie.

5.4. Przykład obliczeniowy

Dane
  1. układ trzech belek połączonych ze sobą blachą trapezową T80/1,25 (Pruszyński)
  2. rozstaw belek wynosi s = 2,5m
  3. szerokość połaci broof = 5m
  4. belka jest elementem swobodnie podpartym o rozpiętości przęsła L = 4,0m
  5. przyjęto belkę o przekroju IPE140 ze stali S235
  6. belki poddane są obciążeniu równomiernemu q = 6,0 kN/m

Wyznaczenie sztywności Sb belki zgodnie z równaniem (W.1): 


Charakterystyki geometryczne dla przekroju IPE140 wykorzystane przy określaniu sztywności Sb można szybko uzyskać wprost z programu z tabeli Przekroje poprzeczne (rys. 6) uwzględniając, że It oraz Iw ze wzoru odpowiada wartościom Ix oraz Iω w tabeli:



Rys. 9. Zrzut ekranu z tabeli „Przekroje poprzeczne” pokazujący wybrane charakterystyki geometryczne przekroju IPE140

Wyznaczenie sztywności S blachy trapezowej
Sztywności postaciowe S typoszeregu blach Pruszyński T80 (t – grubość arkusza blachy) o wysokości przekroju blachy hw = 78 zostały wyznaczone wg (W.4) dla dwóch wariantów:
  1. wariant A – poszycie łączone w co drugiej fałdzie (co skutkuje zgodnie z pkt. BB.2.1 (1)B normy [N1] redukcją S o 80%),
  2. wariant B – poszycie łączone w każdej fałdzie (sztywność wynosi S). 

Zestawione wyniki zostały przedstawione w tabeli 1 w kolumnie 5. Dla każdej wartości S wyznaczono także wartość sztywności podpory bocznej Ry do wprowadzenia przy analizie zwichrzenia (AutoMcr).

Tabela 1. Wyniki analizy wpływu sztywności postaciowej tarczy na nośność analizowanej belki zginanej 



blacha trapezowa
Pruszyński
mocowanie
t
S
Ry
χLT
Mcr
[mm]
[kN]
[kN/m/m]
[-]
[kNm]
1
2
3
4
5
6
7
8
0
pominięcie blachy trapezowej w wymiarowaniu
-
-
-
0.48
10.92
1A
T80
wariant A 
- poszycie łączone 
w co drugiej fałdzie 
(redukcja S o 80%)
0,63
708,4
177,1
0,85
39,21
2A
0,70
829,7
207,4
0,87
42,39
3A
0,75
920,1
230,0
0,88
44,56
4A
0,80
1013,7
253,4
0,89
46,64
5A
0,88
1169,5
292,4
0,90
49,76
6A
1,00
1416,7
354,2
0,91
53,98
7A
1,15
1747,1
436,8
0,92
58,63
8A
1,25
1979,8
495,0
0,92
61,43
1B
wariant B 
- poszycie łączone 
w każdej fałdzie
0,63
3542,0
885,5
0,95
75,78
2B
0,70
4148,4
1037,1
0,96
80,47
3B
0,75
4600,7
1150,2
0,96
83,81
4B
0,80
5068,4
1267,1
0,96
87,21
5B
0,88
5847,3
1461,8
0,97
92,67
6B
1,00
7083,3
1770,8
0,98
101,00
7B
1,15
8735,3
2183,8
0,99
111,63
8B
1,25
9899,2
2474,8
0,99
118,80


Wyniki i wnioski
  1. W analizowanym przykładzie pełną stabilizację translacyjną belki (S > Sb=7912,7kN) zapewniają tylko dwie blachy trapezowe łączone w każdej fałdzie: T80/1,15 oraz T80/1,25. Pozostałe analizowane blachy z Tablicy 1 zapewniają niepełną stabilizację (tzw. stabilizację sprężystą), która może zostać wykorzystana w AxisVM przy wymiarowaniu prętowych elementów stalowych.
  2. Już samo spełnienie warunku dla ciągłego stężenia bocznego S > Sb (W.1) bez weryfikacji warunku ciągłego stężenia przeciwskrętnego Cϑ,k ≥ Cb (W.2) powoduje zwiększenie współczynnika χLT z wartości 0,48 na 0,99 (w analizowanym przykładzie).
  3. Niepełna stabilizacja (S < Sb) zwiększa wielkość momentu krytycznego Mcr belki powodując (w analizowanym przykładzie) wzrost współczynnika χLT przynajmniej o 77% (z wartości 0,48 do 0,85).
  4. Powyższe wyniki wskazują, że w inżynierskiej praktyce projektowej obliczanie sztywności obrotowej Cϑ,k blachy nie ma większego uzasadnienia, bo już samo stężenie boczne znacząco podnosi nośność analizowanej belki. Za stwierdzeniem tym przemawia również fakt, że jest to czynność bardzo pracochłonna. Dodatkowo przedstawione w normie [N2] wytyczne nawiązują do wyników badań doświadczalnych, stąd mają ograniczony zakres stosowalności. 

Na podstawie powyższych wniosków można znacznie zredukować poziom skomplikowania i czasochłonność określenia wpływu stabilizacji belki za pomocą blachy trapezowej. 
Cały tok obliczeń sprowadza się jedynie do wyznaczenia sztywności poszycia S oraz wprowadzenia uzyskanej wartości sztywności Ry jako podpory bocznej w AutoMcr na etapie wymiarowania belki stalowej. Pominąć można wyznaczenie sztywności belki Sb oraz sztywności obrotowej poszycia Cϑ,k , co z pewnością prowadzi do wyników bardziej konserwatywnych.

Łyżka dziegciu w beczce miodu
Włączenie poszycia z blachy trapezowej do współpracy przy stabilizacji elementów ściskanych i zginanych powinno pociągać za sobą systematyczną ocenę stanu technicznego poszycia. Wynika to z występowania w takim przypadku sił prostopadłych do łączników, które mogą prowadzić do owalizacji otworów. Zjawiska tego, ani jego efektów w zadanej perspektywie czasowej, nie jesteśmy w stanie bezpośrednio uwzględnić w wymiarowaniu (aktualnie brak wytycznych), co może znacząco wpłynąć na koszt eksploatacji obiektu. Dodatkowo na niekorzyść trwałości połączeń działa zmienno-znakowość obciążenia wiatrem na poszycie.

6. Płyta warstwowa jako stężenie belki

W przypadku płyty warstwowej podobnie jak dla blachy trapezowej możemy określić jej:
  1. sztywność postaciową S do wyznaczenia sztywności ciągłego stężenia bocznego (podparcie translacyjne),
  2. sztywność obrotową Cϑ,k do wyznaczania sztywności ciągłego stężenia przeciwskrętnego (podparcie ze względu na obrót).

Wartości powyższych sztywności, należy określać w oparciu o wytyczne dokumentu pt. European Recommendations on the Stabilization of Steel Structures by Sandwich Panels [3]. Należy pamiętać, że wymieniona powyżej rekomendacja może być wykorzystana przy spełnieniu następujących kryteriów: 
  1. sztywność łącznika nie może być najsłabszym ogniwem tj. nie może decydować o nośności,
  2. łącznik musi być łącznikiem przelotowym tj. przechodzi przez całą grubość płyty,
  3. odległość łączników od krawędzi płyty warstwowej nie może być mniejsza niż 20 mm. 

6.1. Sztywność postaciowa S płyty

Sztywność postaciową S płyty warstwowej zgodnie ze wspomnianym dokumentem ([N3], wzór 16) określona jest przez poniższą zależność: 


(W.6)

gdzie:
kv – sztywność łącznika określana na podstawie tabeli 1 wg [3],
L – długość usztywnianego elementu,
n – liczba płyt warstwowych,
m – liczba usztywnianych belek,
nk – liczba par łączników przypadających na płytę warstwową,
ck – rozstaw łączników zgodnie z rysunkiem 10.

Rys. 10. Rozstaw łączników w płycie warstwowej wg [3]

Tabela 2. Sztywność kv [kN/mm] łącznika wg [N3] (dla grubości konstrukcji tc,s do 4 mm = w pozostałych przypadkach należy sztywność kv obliczyć)
grubość okładziny wewnętrznej tF2
S220GD
S280GD
S320GD
0,40 mm
1,6
1,9
2,0
0,50 mm
2,0
2,3
2,5
0,63 mm
2,4
2,9
3,1
0,75 mm
2,8
3,3
3,6


Warto zauważyć, że w przypadku płyt warstwowych sztywność łącznika ma bezpośredni wpływ na sztywność postaciową płyty (zależności takiej nie ma dla blachy trapezowej). Wynika to między innymi z ich znacznej długości i smukłości. Sztywność łącznika zgodnie z [3] określamy w następujący sposób ([N3], wzór 21): 


 (W.7)

gdzie:


kF2 – sztywność okładziny wewnętrznej: 
 dla   lub
  dla 
tc,s  – grubość rdzenia podkonstrukcji,
D – grubość płyty warstwowej,
Cs – sztywność rotacyjna zamocowania łącznika w podkonstrukcji:

EI – sztywność giętna rdzenia łącznika:

fu,F2 – wytrzymałość na rozciąganie okładziny wewnętrznej,
tc,F2 – grubość rdzenia okładziny wewnętrznej,
d1 – mniejszy wymiar gwintowanej średnicy trzpienia łącznika,
ds – średnica niegwintowanej części łącznika.

Praktyczny zakres stosowania powyższej przedstawionych wzorów jest ograniczony dla:
  1. łączników o średnicy nominalnej d0 w przedziale od 5,5 mm do 8 mm, 
  2. grubości płyty warstwowej D od 40 mm, 
  3. grubości rdzenia stalowej okładziny wewnętrznej tc,F2 od 0,4 mm do 1,0 mm,
  4. grubość rdzenia stalowej podkonstrukcji tc,s od 1,5 mm do 10,0 mm.

W przypadku stabilizowania belek płytami warstwowymi należy dodatkowo sprawdzić warunek dopuszczalnego kąta obrotu γ pomiędzy płytą warstwową a stabilizowaną belką (Rys. 10). 

      oraz     
(W.8)
gdzie: 
e0 – wstępna imperfekcja geometryczna,
L – rozpiętość stabilizowanej belki,
Si – sztywność postaciowa poszycia,
Fi – siła ściskająca w pasie belki.

6.2. Sztywność obrotowa C płyty

Wyznaczenie sztywności obrotowej poszycia wykonanego z płyty warstwowej może być przeprowadzone poprzez zastosowanie alternatywnego wzoru podanego w [N2], wzór 10.16 


(W.9)

gdzie:
k – współczynnik liczbowy, zależny od umiejscowienia belek,
E – średni moduł sprężystości belki,
Ieff – efektywny moment bezwładności przekroju poszycia na jednostkę długości,
w przypadku płyty warstwowej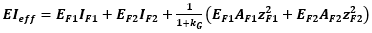 
 
oraz 

EF1, EF2 – moduł sprężystości odpowiednio okładziny zewnętrznej i wewnętrznej,
IF1, IF2 – moment bezwładności odpowiednio okładziny zewnętrznej i wewnętrznej,
AF1, AF2 – pole przekroju odpowiednio okładziny zewnętrznej i wewnętrznej,
zF1, zF2 – odległość środka ciężkości odpowiednio okładziny zewnętrznej i wewnętrznej od środka ciężkości płyty,
GC – moduł sprężystości poprzecznej rdzenia,
s – rozstaw belek.

6.3. Przykład obliczeniowy

Dany jest układ 3 belek, na których opiera się płyta warstwowa PWS-PIR-ST-100. Rozstaw belek wynosi B = 2,34 m. Belka jest elementem swobodnie podpartym o rozpiętości przęsła L = 4,0 m. Wstępnie przyjęto belkę o przekroju IPE140, ze stali S235. Belki poddane są obciążeniu równomiernemu q = 6,0 kN/m.

Sztywność belki Sb zostanie określona zgodnie z równaniem (W.1): 


Dane materiałowe płyty PWS-PIR-ST-100: 
  1. okładziny – stal S280, grubość nominalna obu okładzin tF = 0,5 mm. 
  2. grubość nominalna całkowita płyta D = 100 mm
Wyznaczenie sztywności postaciowej płyty S


gdzie: 
L = 4000 mm
n = 4 (zostaną położone 4 płyty)
m = 3 (liczba usztywnianych belek)
nk = 2 (przyjęto 4 łączniki na szerokości) 
ck = 1000 mm i 400 mm (patrz Rysunek) 


Rys. 11. Rozstaw łączników w analizowanym przypadku

kv – należy określić poniższym wzorem (grubość półki dwuteownika jest większa niż 4 mm stąd nie można skorzystać z Tabeli 2.) 


gdzie: 
D = 100 mm
tc,s = 6,9 mm
d1 = 4,4 mm

Rys. 12. Parametry geometryczne analizowanego łącznika




fu,F2 = 360N/mm2
tc,F2 = 0,4 mm (odjęto grubość powłok cynkowych i ochronnych ~0,1 mm)






Podsumowanie

Wyznaczona sztywność S płyty dotyczy analizowanej połaci. Do celów oceny efektywności usztywnienia pojedynczej belki musi ona zostać podzielona przez m (liczba usztywnianych belek).

W analizowanym przykładzie sztywność postaciowa pokrycia przypadająca na analizowaną belkę jest mniejsza od sztywności belki (S = 3617,5kN / 3 = 1205,8kN < Sb = 7912,7kN). Oznacza to sprężyste podparcie translacyjne belki IPE 140 o wartości 1205,8kN na długości belki (4m), co daje wartość sztywności podpory bocznej do wprowadzenia w programie równą 301,5kN/m.

7. Płyta żelbetowa jako stężenie belki

7.1. Definicja

Każda belka, która ma współpracować z płytą lub powłoką automatycznie zostaje zdefiniowana przez program AxisVM jako elementy typu żebro. W odróżnieniu od elementu typu pręt, który jest elementem Bernoulli, żebro jest elementem Timoshenko. Z racji współpracy żebra z elementem powierzchniowym możliwe jest sprawne, za pomocą jednego kliknięcia, ustawienie mimośrodu belki względem płaszczyzny płyty/powłoki. Zgodnie z przedstawionym poniżej rysunkiem żebro może być zdefiniowane w kolejności jako podciąg, nadciąg, jako żebro w środku lub jako żebro z mimośrodem zdefiniowanym przez użytkownika, czyli dowolnym.


Rys. 13. Określanie mimośrodu dla belki stalowej względem płyty żelbetowej w AxisVM

W przypadku położenia podciąg i nadciąg użytkownik może dodatkowo określić sztywność „wzdłużną” połączenia ścinanego belka – płyta. Dostępne są dwa warianty tego połączenia: 
  1. połączenie sztywne z domyślnie określoną sztywnością kx = 1×106 [kN/m/m], 
  2. połączenie sprężyste ze sztywnością kx określaną przez użytkownika.

7.2. Parametry przy wymiarowania stali (zwichrzenie)

W przypadku zamodelowania belki stalowej połączonej z płytą żelbetową, podparcie belki w jej analizie zwichrzenia w AutoMcr zawsze lokalizowane będzie domyślnie wzdłuż osi środkowej belki, niezależnie od zadanego mimośrodu belki względem płyty. Lokalizację podpór bocznych symbolizują niebieskie znaczniki na widoku podłużnym belki. Wartość mimośrodu można ustawić w pożądanym miejscu na wysokości belki poprzez edycję domyślnej wartości w kolumnie Mimośród. Jeżeli podpora ma zostać przesunięta na górną lub dolną krawędź belki, zamiast wpisywać wartość numeryczną przesunięcia, można użyć wpisu h/2 lub -h/2, aby program uzupełnił tę wartość samodzielnie na podstawie przyjętego profilu stalowego.


Rys. 14. Automatycznie przyjęte parametry podpór do analizy zwichrzenia belki zespolonej z płytą żelbetową

Niezależnie od sztywności giętnej płyty jak i niezależnie od sztywności połączenia ścinanego kx na styku tych elementów, program zawsze przypisuje wymiarowanej belce pełną blokadę zarówno translacyjną Ry jak i rotacyjne Rxx i Rzz (rys. 14). 

Dlatego, gdy nie ma pewności co do zapewnienia przez płytę sztywności obrotowych lub nie są wymagane szczegółowe analizy w tym kierunku, sugeruje się modyfikację automatycznie przyjętych sztywności poprzez wyzerowanie sztywności obrotowych Rxx i Rzz. Podejście takie jest podejściem konserwatywnym, ale w standardowych sytuacjach obliczeniowych przy obliczeniach inżynierskich wystarczającym.
Bardziej szczegółowe informacje dotyczące zabezpieczenia belek zespolonych przed zwichrzeniem, jak i zasady określania sztywności połączenia płyta-belka można znaleźć w [N6].

Bibliografia

[N1] PN-EN 1993-1-1:2006, Projektowanie konstrukcji stalowych -- Część 1-1: Reguły ogólne i reguły dla budynków.
[N2] PN-EN 1993-1-3:2008, Projektowanie konstrukcji stalowych, Część 1-3: Reguły ogólne – Reguły uzupełniające dla konstrukcji z kształtowników i blach profilowanych na zimno.
[N3] PN-EN 1090-4:2018, Wykonanie konstrukcji stalowych i aluminiowych Część 4: Wymagania techniczne dotyczące profilowanych na zimno stalowych elementów konstrukcyjnych oraz konstrukcji poszycia dachów, sufitów, stropów i ścian.
[N4] prEN 14509-2:2016, Double skin metal faced insulating panels. Factory made products. Specifications. Part 2: Structural applications - fixings and potential uses of stabilization of individual structural elements.
[N5] ENV 1993-1-1:1992 Eurocode 3, Design of steel structures. General rules and rules for buidings
[N6] PN-EN 1994-1-1:2008 Projektowanie zespolonych konstrukcji stalowo-betonowych, Część 1-1: Reguły ogólne i reguły dla budynków.

[1] Ciesielczyk, K., Chuda-Kowalska, M.,Studziński, R. (2020) Obudowa ścian i dachów – rodzaje i kształtowanie elementów nośnych, Konstrukcje metalowe, posadzki przemysłowe, lekka obudowa, rusztowania. Tom 2 – Materiały, nowoczesne technologie, realizacje konstrukcji stalowych, str. 61-106, Akademia Techniczno-Humanistyczna w Bielsku-Białej. 
[2] European recommendations for the application of metal sheeting acting as a diaphragm’ by European Convention for Constructional steelwork (ECCS) No.88
[3] CIB Publication 379, European Recommendations on the Stabilization of Steel Structures by Sandwich Panels, 2014, ISBN 978-90-6363-081-2 
[4] SN003a-PL-EU, Informacje uzupełniające: Sprężysty moment krytyczny przy zwichrzeniu
[5] AxisVM X5 Podręcznik użytkownika
[6] Bródka J., Garncarek R., Miłaczewski K. Blachy fałdowe w budownictwie stalowym, Arkady, 1999



    • Related Articles

    • Obciążenia imperfekcyjne wydzielonych układów stężeń

      1. Wprowadzenie Poprawnie zaprojektowany płaski układ prętowy jest samostateczny i geometrycznie niezmienny w „swojej płaszczyźnie”, (tj. płaszczyźnie -XZ-) będąc jednocześnie geometrycznie zmiennym w płaszczyźnie -YZ- (patrz rys. 1.)   Rys. 1. Widok ...

    • Metoda ogólna wymiarowania elementów stalowych wg EC3

      zalecenia, zakres stosowania, algorytm, przykłady obliczeniowe 1. Kiedy należy stosować metodę ogólną? Norma PN-EN 1993-1-1:2006 umożliwia sprawdzenie stateczności z płaszczyzny elementów zginanych i ściskanych metodą ogólną (punkt 6.3.4) . ...

    • Wymiarowanie rygla ramy portalowej z dachem dwuspadowym

      1. Podparcie rygla Podczas wymiarowania rygla ramy portalowej z dachem dwuspadowym często przyjmuje się bez głębszej analizy, że podparcie rygla w płaszczyźnie układu stanowią słupy. Przyjęte podparcie w płaszczyźnie układu wpływa bezpośrednio na ...

    • Liniowa analiza wyboczeniowa - założenia i praktyczne zastosowania

      Założenia LBA Liniowa analiza wyboczeniowa (ang.linear buckling analysis - LBA ) pozwala na określenie postaci wyboczenia konstrukcji i odpowiadających im wartości własnych . Założenia liniowej analizy wyboczeniowej są następujące: obciążenie jest ...

    • Wybór analizy globalnej dla stalowej konstrukcji ramowej

      Algorytm wyboru analizy statycznej oraz weryfikacji nośności ramowej konstrukcji stalowej w zależności od uzyskanego mnożnika krytycznego αcr. Dla różnych wariantów wybierano zawsze analizę możliwie najniższego rzędu., co nie wyklucza zastąpienia jej ...