1. Kiedy należy stosować metodę ogólną? 

Norma PN-EN 1993-1-1:2006  umożliwia sprawdzenie stateczności z płaszczyzny elementów zginanych i ściskanych metodą ogólną (punkt 6.3.4) . Sprawdzenie takie nabiera znaczenia wtedy, kiedy powszechnie stosowane wymiarowanie elementu wydzielonego za pomocą wzorów przytoczonych w punktach

1. 6.3 Stateczność elementów pełnościennych
1. 6.3.1 Elementy ściskane o stałym przekroju, 
2. 6.3.2 Elementy zginane o stałym przekroju
3. 6.3.3 Elementy zginane i ściskane o stałym przekroju. 
   

nie spełnia warunków tam przedstawionych. Wspólnym mianownikiem przytoczonych weryfikacji jest bowiem element o stałym przekroju (w literaturze nazywany też jako pręt pryzmatyczny) i tylko dla takiego pręta uzyskamy miarodajne wyniki wg wytycznych przedstawionych w powyższych punktach .

Sytuacja, kiedy powinniśmy zastosować metodę ogólną pojawia się najczęściej przy analizowaniu stateczności elementów ze zbieżnym przekrojem . Przekroje takie często znajdują zastosowanie przy projektowaniu ram stalowych budynków halowych. Powszechnie stosuje się pełnościenny rygiel ze zbieżnym przekrojem w strefie przyokapowej. Wprowadzenie w tym miejscu rygla o zmiennej wysokości jest wysoce uzasadnione i związane jest z przebiegiem momentów zginających (dostosowaniem wysokości przekroju to wartości momentu zginającego) oraz z koniecznością zwiększenia ramienia sił wewnętrznych dla styku doczołowego rygiel-słup (zapewnienie zakładanej nośności i sztywności połączenia). 

Rys. 1. Wzmocnione przekroje poprzeczne rygla

Zakres stosowania metody ogólnej umożliwia ocenę stateczności elementów z przekroi pojedynczych lub złożonych , zarówno o stałym jak i zmiennym przekroju poprzecznym i różnych warunkach podparcia . Co ważne, daje również możliwość oceny całych ram płaskich jak i podzespołów tych ram złożonych ze wspomnianych elementów.  Warunkiem jaki muszą te elementy spełnić wg normy jest ich ściskanie i/lub jednokierunkowe zginanie w płaszczyźnie . Dodatkowo z zastrzeżeniem, że zginanie ma charakter sprężysty (można przyjmować nośności plastyczne przekroju, ale nie należy przeprowadzać analizy plastycznej z redystrybucją momentów). 

Na podstawie analizy statycznej odczytujemy z programu zestaw sił w przekroju krytycznym. Następnie wyznaczamy minimalny mnożnik amplifikacji obciążeń obliczeniowych, przy którym przekrój krytyczny osiąga nośność charakterystyczną w warunkach płaskiego stanu deformacji z uwzględnieniem właściwych imperfekcji geometrycznych. Mnożnik α _ult,k  można wyznaczyć wg punktu 6.4.3 (4) [N1]

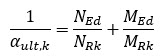
Jest to parametr amplifikacji obciążenia obliczeniowego w odniesieniu do nośności charakterystycznej najbardziej wytężonego przekroju analizowanego komponentu z uwzględnieniem niestateczności w płaszczyźnie tj. wszystkich efektów spowodowanych deformacją i imperfekcjami (globalne, lokalne) elementów w płaszczyźnie, tam gdzie ma to zastosowanie.

_{Jest to mnożnik, przy którym rozpatrywana część konstrukcji osiąga wartość obciążenia krytycznego przy niestateczności sprężystej z płaszczyzny układu. Wartość jego wyznaczamy za pomocą analizy wyboczeniowej (LBA), ale konieczne jest wykorzystanie prętów 7DoF lub modelu powłokowego (ze względu na konieczność uwzględnienia spaczenia i deformacji giętno-skrętnej elementu).}

Wartość globalnej smukłości względnej części składowej ma postać

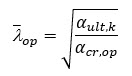
Jest to mniejsza z wartości χ _z   i  χ _LT   określonych dla globalnej smukłości względnej.

Korzystając z metody ogólnej należy mieć na uwadze też to, że w literaturze przedmiotu odnaleźć można artykuły, w których przedstawione przykłady walidujące prowadzą do wyników satysfakcjonujących [1] , niesatysfakcjonujących [2] oraz takich, które wskazują na niespójność metody ogólnej w stosunku do rozwiązań ścisłych (uzyskanych np. przy pomocy analizy GNIA) [3] . 

W poniższej tablicy przedstawiono porównanie „punktów charakterystycznych” wymiarowania wg  PN-EN 1993-1-1 pkt.  6.3.3 - metoda elementów wydzielonych z wymiarowaniem wg 6.3.4 - metoda ogólna

Tablica 1. Porównanie „punktów charakterystycznych” wymiarowania wg EC3 6.3.3 i 6.3.4

Procedura	Metoda elementów wydzielonych [6.3.3]	Metoda ogólna [6.3.4]
Wyznaczenie decydujących obliczeniowych sił wewn.	N  Ed  ,  M  y,Ed dla elementu	N  Ed  ,   M  y,Ed dla przekroju krytycznego
Nośność	N  Rk  ,  M  Rk
Nośność krytyczna	N  cr  ,  M  cr	α    cr,op
Smukłość względna
Współczynniki niestateczności	χ  z   , χ  LT	χ  op   = min {χ  z   ; χ  LT  }
Współczynniki interakcji	k  zy	-
Weryfikacja

3. Arkusz online

W celu usprawnienia obliczeń przygotowaliśmy arkusz online, który jeszcze bardziej przyspiesza obliczenia i sprowadza wymiarowanie do kilku kroków w programie AxisVM.

Gotowy arkusz do wymiarowania metodą ogólną znajdziesz tutaj

https://axisvm.help.gammacad.pl/portal/pl/kb/articles/arkusz-do-wymiarowania-metoda-ogolna-wg-ec3

Zadanie przeliczono dwutorowo, zgodnie ze schematem przedstawionym w Tablicy 1. 

4.1.1. Wymiarowanie elementu wydzielonego wg 6.3.3 PN-EN 1993-1-1 dla klasy 3 przekroju

Przeprowadzając wymiarowanie dla całego elementu uzyskano stopień wykorzystania elementu dla  SGN = 0,580

4.1.2. Wymiarowanie metodą ogólna 

1. Krok 1
   W wyniku przeprowadzonej analizy statycznej wyznaczono siły w przekroju krytycznym  M _y,Ed  = 125kNm i  N _Ed  = 100kN. Stąd uwzględniając nośności przekroju na ściskanie i zginanie sprężyste otrzymamy
   
   
   
2. Krok 2
   Za pomocą analizy wyboczeniowej dla pręta 7DoF, dla którego możliwe jest uwzględnienie spaczenia i deformacji giętno-skrętnej, otrzymano wartość  α  _cr,op = 3,301 dla pierwszej postaci wyboczenia
   
   

Rys. 4. Postać z analizy wyboczenia dla pręta 7 DoF

1. Krok 3
   Wyznaczenie  globalnej smukłości względnej  części składowej
   
   
   

2. Krok 4
   Wyznaczenie współczynnika niestateczności jako mniejszej z dwóch poniższych wartości
   
   
   
   
   
   
   
   

3. Krok 5
   Warunek stateczności
    

4.1.3 Porównanie wyników obu metod dla przykładu 1

Wymiarowanie metodą elementu wydzielonego doprowadziło do wyniku wykorzystania na poziomie 58,0%, a metodą ogólną do wartości 58,6% (różnica na poziomie 1%).

4.2. Przykład 2

1. belka utwierdzona z jednej strony i przegubowo podparta z drugiej
   
2. stały przekrój na całej długości (IPE 450)
   
3. długość belki L=10,0m
4. obciążenie równomiernie rozłożone 10kN/m; siła skupiona 100kN na jednym końcu i moment skupiony 50kNm na drugim
   
5. podparcie boczne na wysokości pasa górnego w połowie rozpiętości

4.2.1. Wymiarowanie elementu wydzielonego wg 6.3.3 PN-EN 1993-1-1 dla klasy 3 przekroju

Przeprowadzając wymiarowanie dla całego elementu uzyskano stopień wykorzystania elementu dla SGN = 0,626 

4.2.3 Porównanie wyników obu metod dla przykładu 2

Stopień wykorzystania dla metody wg elementu wydzielonego wynosi 62,6%, a dla metody ogólnej 64,8% (różnica na poziomie 3,4%).

Zwróć uwagę, że tak zamodelowana belka przysparza wiele problemów przy obliczaniu metodą elementów wydzielonych. Wynika to z faktu, że możliwe do wyodrębnienia elementy do wymiarowania nie są pryzmatyczne - brak możliwości jednoznacznego przypisania charakterystyk geometrycznych przekroju (zmiana profilu na długości). Dlatego norma nie obejmuje wymiarowania takich elementów metodą elementów wydzielonych (EC3 pkt. 6.3.1-6.3.3).

Prezentowany układ jest rozwinięciem wcześniejszych zadań. Tym razem rygiel z jednej strony, zamiast podpory węzłowej otrzymał oparcie na słupie. W przykładzie tym za pomocą metody ogólnej sprawdzony zostanie cały układ, a co za tym idzie, stopień wykorzystania będzie odnosił się również do całego układu - nie wyodrębnia się osobno wykorzystania dla rygla i słupa, ponieważ analiza wyboczeniowa dotyczy całego układu. 

Do problemów przy wymiarowaniu metodą elementów wydzielonych wspomnianych w przykładzie 3, w kontekście bieżącego zadania dodać należy brak możliwości wiarygodnego wyznaczenia momentu krytycznego dla rygla i słupa. Jest to spowodowane brakiem podparcia bocznego w miejscu ich połączenia.