1. Wprowadzenie

1. redukowaniem długości wyboczeniowych elementów ściskanych i/lub zginanych,
2. „przenoszeniem” obciążeń poziomych od wiatru i urządzeń transportowych oraz
3. „przenoszeniem” sił od imperfekcji geometrycznych stężanych elementów.

1.1 Klasyfikacja stężeń w układach halowych

1.2 Stężenia w układach płaskich

1.2.1 Model imperfekcyjny steżęń w Eurokodzie 3

(W.1)    [5.3.3 (1) EC3-1-1]

L   jest rozpiętością stężenia,

α_m   wyrażone jest wzorem: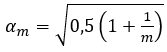

m   jest liczbą stężanych elementów

(W.2)     [5.3.3 (2) EC3-1-1]

N_Ed,i   jest siłą ściskającą w elemencie podpieranym (stężanym),

e₀   jak w równaniu (R.1),

δ_q   jest ugięciem stężenia od oddziaływania q_d i wszelkich obciążeń zewnętrznych uzyskanych z analizy I-go rzędu (ustalenie właściwej wartości δ_q następuje na drodze iteracyjnej, co zostało przedstawionej w dalszej części). 

Dla innych warunków podparć niż belka swobodnie podparta konieczne jest zarówno zmodyfikowanie wyrażenia na strzałkę ugięcia e ₀ jak i wyprowadzenie odpowiedniego wzoru na wartość obciążenia imperfekcyjnego q _d (patrz kolejne przykłady).

Interpretacja siły N _Ed we wzorze na wstępną imperfekcję łukową

1. w przypadku elementu tylko ściskanego (np. pas górny kratownicy) siła N_Ed równa jest największej sile ściskającej w stężanym elemencie N_Ed = N_Ed,max
2. w przypadku elementu zginanego (zginana belka stropowa o wysokości przekroju h) siła N_Ed jest wyznaczana z momentu zginającego N_Ed = M_Ed,max/h 
3. w przypadku elementu zginanego i ściskanego (rygiel pełnościenny ramy) siła NEd wyznaczana jest ze wzoru N_Ed = M_Ed,max/h + 0,5N_Ed,max
   

1.2.2 Dodatkowa siła w w miejscu styków montażowych

(W.3)   [5.3.3 (4) EC3-1-1]

N_Ed jak w równaniu (W.2),

α_m jak w równaniu (W.1). 

1.2.3 Algorytmy projektowania stężeń wg Eurokodu 3 w odniesieniu do układów wydzielonych 

1.3 Stężenia w układach przestrzennych

2. Połaciowe stężenia poprzeczne - przykład obliczeniowy

1. polaciowe-stezenie-poprzeczne-wiotkie-warA.axs
2. polaciowe-stezenie-poprzeczne-sztywne-warB.axs

Plik zawiera tylko model. Konieczne jest przeprowadzenie analizy w celu uzyskania wyników.

2.1 Informacje wstępne o obiekcie

Samo graniczne kryterium smukłości dla elementów ściskanych nie jest sprecyzowane w Eurokodzie 3. W literaturze elementy bardzo smukłe wiązane są ze smukłością λ ≥ 200, λ ≥ 220 lub λ ≥ 250 (ostatnia z tych wartości była określona w normie PN-90/B-03200 - dalej [N2]).

 

2.2 Kroki obliczeń

1. wariant A – stężenie z prętami wiotkimi
   
2. wariant B – stężenie z prętami sztywnymi
   

Krok 1 - przyjęcie układu wydzielonego

Pas górny i dolny układu wydzielonego jest odpowiednio zorientowanym przekrojem pasa górnego kratownicy z naszego zadania.

 

Krok 2 - ustalenie układu statycznego

W drugim kroku ustalamy warunki brzegowe i schemat statyczny. W naszym przypadku podporami dla analizowanego stężenia połaciowego będą stężenia pionowe podłużne słupów. 

Rys. 6a. Układ wydzielony stężenia połaciowego poprzecznego w wariancie A (pręty wiotkie stężenia)

 

 

Rys. 6b. Układ wydzielony stężenia połaciowego poprzecznego w wariancie B (pręty sztywne stężenia)

 

Krok 3 - zebranie obciążeń poziomych

W trzecim kroku przyjęte zostaje obciążenie poziome. W naszym przypadku jest to obciążenie wiatrem ze ściany szczytowej. Przy ustalaniu obciążenia wiatrem przyjęto stałą wartość parcia wiatru na ścianę szczytową równą 0,4 kN/m ² (wartość obliczeniowa). Obciążenie to przekazywane jest przez słupki wiatrowe ściany szczytowej w postaci sił skupionych (słupek ściany szczytowej ma schemat elementu obustronnie przegubowo podpartego – połowa obciążenia wiatrem przypada na fundament a druga na stężenie połaciowe poprzeczne).

 

Rys. 7. Obciążenia skupione od działania wiatru na ścianę szczytową

 

Krok 4 - iteracyjne wyznaczenie obciążenia imperfekcyjnego

W czwartym kroku należy ustalić wartość obciążeń imperfekcyjnych wg równania (W.2) i ew. (W.3).

Przy ustalaniu wartości obciążenia w zadaniu przyjęto siłę ściskającą w pasie górnym kratownicy N_Ed = -300 kN. 

 

We wzorze na q_d należy zwrócić uwagę na parametr m który określa liczbę stężanych układów przypadającą na stężenie. W naszym przypadku mamy 8 ram (2 skrajne i 6 pośrednich). Skrajne układy poprzeczne w przypadku jednakowych rozstawów ram przejmują 50% obciążenia przejmowanego przez układy pośrednie. Skrupulatnie określając wartość m możemy ten fakt wykorzystać, co da nam wartość m = 3 + 0,5 = 3,5. W przykładzie przyjęto wartość m = 4,0.

Rys. 8. Przyjęcie liczby stężanych elementów

 

Poniżej przedstawiono przebieg iteracji do wyznaczania obciążenia q_d wg wzoru (W.2) dla obliczonych parametrów zadania:

α_m=0,79; e₀ =31,6mm; m=4; N_Ed = -300 kN

Obliczenia dla wariantu A - stężenia wiotkie

W tym przypadku statykę należy rozwiązać jako problem nieliniowy, gdyż stężenia wiotkie pracują tylko na rozciąganie. 

 

Rys. 9. Uruchomienie analizy nieliniowej dla wariantu A

1. δ_q (brak - pierwszy krok iteracji); 
   q_d = 0,76kN/m
   Przemieszczenia węzła po wykonaniu analizy nieliniowej wynosi 6,146mm (~6,1mm)
2. δ_q =6,1mm
   q_d(2) = 0,91kN/m
   Przemieszczenia węzła po wykonaniu analizy nieliniowej wynosi 6,573mm (~6,6mm)
3. δ_q =6,6mm
   q_d(3) = 0,92kN/m
   Przemieszczenia węzła po wykonaniu analizy nieliniowej wynosi 6,635mm (~6,6mm)
4. δ_q =6,6mm
   q_d(4) = 0,92kN/m 
   Koniec iteracji - q_d(4) = q_d(3)

Odczyt przemieszczeń przeprowadzono w środkowym węźle obciążonego elementu stężanego.

 

Obliczenia dla wariantu B - stężenia sztywne

Analiza liniowa jest wystarczająca dla tego zagadnienia.

 

Rys. 10. Uruchomienie analizy liniowej

 

1. δ_q (brak - pierwszy krok iteracji); 
   q_d = 0,76kN/m
   Przemieszczenia węzła po wykonaniu analizy liniowej wynosi 1,166mm (~1,2mm)
2. δ_q =1,2mm
   q_d(2) = 0,79kN/m
   Przemieszczenia węzła po wykonaniu analizy liniowej wynosi 1,183mm (~1,2mm)
3. δ_q =1,2mm
   q_d(3) = 0,79kN/m
   Koniec iteracji - q_d(3) = q_d(2)

Odczyt przemieszczeń przeprowadzono w środkowym węźle obciążonego elementu stężanego.

Zgodnie z uwagą w 5.3.3 (2) EC3 można przyjmować δ_q =0 (pominąć iterację), jeżeli układ stężeń zostanie policzony wg teorii drugiego rzędu, czyli z włączoną opcją Geometryczna nieliniowość w analizie nieliniowej.

Krok 5 - weryfikacja SGN

Po każdym kroku iteracyjnym weryfikowany jest stan SGN elementów stężenia. Należy również pamiętać, aby siłę ściskającą w pasie górnym powstałą z analizy stężeń „dodać” do siły w pasie górnym kratownicy. 

W przypadku stężenia w wariancie A i wariancie B dodatkowa siła ściskająca w pasie górnym kratownicy układu poprzecznego (odczytana z ostatniego kroku iteracji stężeń) wynosi odpowiednio N_Ed,add = -21,9 kN i N_Ed,add = -17,1 kN . Ostatecznie pas górny kratownicy należy zaprojektować na siłę N_Ed,tot = N_Ed + N_Ed,add . 

W miejscach styków montażowych należy uwzględnić lokalne oddziaływanie F określone równaniem (W.3) . W zadaniu siłę F = 0,01×0.79×300 = 2,37 kN przyłożono w środku rozpiętości analizowanego stężenia. Wytężenie stężenia będzie niższe przy obciążeniu siłą F niż przy obciążeniu q_d dlatego wpływ tego obciążenia pominięto w przykładzie.

Krok 6 - weryfikacja SGU

Stan SGU sprawdzamy po zakończeniu procedury iteracyjnej i weryfikacji stanu SGN. 

Warunek sztywności stężenia nie jest obligatoryjny, ani wyrażony w EC3.

Poniżej przedstawiono zalecane równanie do weryfikacji sztywności stężenia z normy [N2] p. 5.2 a)

(W.4)

 

gdzie:

δ = δ_j - d_i jest maksymalnym wzajemnym przemieszczeniem dwóch sąsiednich węzłów kratownicy stężenia,

b = b_j - b_i jest odległością między sąsiednimi węzłami.

Sprawdzenie sztywności zaprezentowano na przykładzie A (ze stężeniami wiotkimi).

Rys. 11. Globalne przemieszczenia wydzielonego układu stężenia

W omawianym przykładzie na podstawie wyników przemieszczeń globalnych (rys. 11) wytypowano do sprawdzenia przemieszczenia węzłów pręt [51] oraz [22].

 

Rys. 12. Względne przemieszczenia węzłów pręta [51]

 

 

Rys. 13. Względne przemieszczenia węzłów pręta [22]

 

Największe względne przemieszczenie węzłów występuje w pręcie [22]. Warunek sztywności przyjmuje postać δ/b = 4,5 / 5000 = 0,0009 i jest mniejszy od wartości granicznej wynoszącej 0,005. Stopień wykorzystania wynosi 0,0009 / 0,005 = 18%.

 

3. Ścienne stężenia podłużne pionowe - przykład obliczeniowy

Plik z zadaniem: scienne-stezenie-pionowe.axs

Wymagana min. wersja AxisVM: X5 R4

Plik zawiera tylko model. Konieczne przeprowadzenie analizy w celu uzyskania wyników.

 

 

Rys. 14. Widok aksonometryczny hali

 

3.1 Przyjęcie układu

Dane początkowe zadania są takie same jak w rozdziale 2.

Układ wydzielony wraz z przyjętymi warunkami podparcia ściennego stężenia podłużnego przedstawiony jest na rys. 15. Stężenia pionowe podłużne słupów podpierają stężenie połaciowe poprzeczne, przejmują obciążenie wiatrem ze ściany szczytowej oraz zapewniają stateczność hali w kierunku podłużnym. Wielkość obciążenia zewnętrznego przypadająca na analizowane stężenie w układach wydzielonych równa się reakcji podporowej od obciążenia wiatrem stężenia połaciowego poprzecznego i wynosi R_w = 12,5 kN. Siła ta powinna być przyłożona do głowicy słupa. Dla naszego zadania otrzymamy następujący układ

Rys. 15. Układ wydzielony pionowego stężenia podłużnego słupów

 

3.2 Siła na stężenie od imperfekcji globalnych (przechyłowych)

Wstępny, losowy przechył stężanych słupów hali uwzględniany jest przez wprowadzenie imperfekcji przechyłowej wyrażonej przez siłę poziomą (patrz pkt. 5.3.2 PN-EN 1993-1-1). W przypadku zebrania sił na układ stężenia musimy uwzględnić wpływ ze wszystkich usztywnianych danych stężeniem słupów:

 

(W.5)

 

gdzie

N_Ed,si jest maksymalną siłą ściskającą w słupie,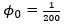

    oraz   

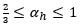h jest wysokością konstrukcji w metrach (w przypadku analizowanego stężenia jest to wysokość słupa – h = 6,0m),

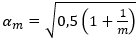m jest liczbą stężanych elementów (w naszym przypadku przyjmujemy m = 4, tak jak dla połaciowych stężeniach poprzecznych).

 

Siła H_i,s przykładana jest do stężenia na poziomie belki okapowej (tak jak reakcja od wiatru). Przy ustalaniu wartości siły H_i,s przyjęto siłę ściskającą w słupie N_Ed,s = -400 kN. Po podstawieniu wartości otrzymujemy

3.3 Siła na stężenie od lokalnych (łukowych) imperfekcji słupów

W przypadku ściennego stężenia pionowego osobnego komentarza wymaga sposób uwzględnienia imperfekcji łukowej słupa. W tym przypadku znaczenia nabiera występowanie lub brak pośrednich tężników stężenia. Rozpatrzymy dwa warianty takiego stężenia:

1. wariant A – stężenie bez tężników pośrednich (taki jak w analizowanej hali)
2. wariant B – stężenie z pośrednimi tężnikami (alternatywnie)

W pierwszej kolejności określona zostanie wartość obciążenia stabilizującego q_d (analogicznie jak w przypadku stężenia połaciowego poprzecznego) według wzoru (W.2), podstawiając za L wysokość słupa. Natomiast strzałkę wygięcia e₀ ( Tab.5.1 [N1]) przyjmuje się wg krzywej wyboczeniowej słupa ( Tab. 6.2 [N1]). W naszym przypadku (słup o wysokości 6m i przekroju IPE 450 wykonany jest ze stali S235) strzałkę wygięcia e₀, zgodnie ze wspomnianą tabelą określa krzywa wyboczenia b.

3.4 Obliczenia dla wariantu A - bez tężników pośrednich (układ analizowanej hali)

W przypadku stężenia bez tężników pośrednich ( rys. 16) imperfekcja łukowa w słupach nie przekazuje się na pręty stężenia (wygięcie łukowe pręta realizuje się między prętami stężenia, a z racji występowania sił przeciwdziałających nie oddziaływuje na stężenia - siły normalne wynoszą 0kN). Innymi słowy nie ma potrzeby przykładania obciążenia stabilizującego na układ stężenia, gdyż nie spełnia ono tutaj żadnej roli.

 

Rys. 16. Widoczny brak wpływu obciążenia stabilizującego na układ stężenia

 

3.5 Obliczenia dla wariantu B - z tężnikami pośrednimi

Sytuacja wygląda inaczej, gdy występują pośrednie tężniki ( rys. 17), gdyż w tym przypadku wygięcie łukowe przekazuje się poprzez te tężniki na pręty stężenia. 

 

Wartość pierwszej iteracji obciążenia q_d na układ stężenia wynosi

i zawiera wpływ z m=4 słupów.

 

Siły przeciwdziałające H_q wynoszą

 

Rys. 17. Wpływ imperfekcji łukowej na układ stężenia z tężnikami pośrednimi (przemieszczenia i siły normalne)

 

3.6 Podsumowanie

W układzie z analizowanego zadania należy zatem przyłożyć siłę od obciążeń poziomych ( R_w =12,50kN) oraz zastępczą siłę od przechyłu słupów ( H_i,s =5,16kN). Zastępcza siła od działania imperfekcji łukowej w tym przypadku nie musi być uwzględniana, co udowodniono powyżej. Aby uzyskać prawidłowe wyniki dla tak przygotowanego układu wystarczy uruchomić analizę liniową, gdyż w tym układzie zastosowano stężenia sztywne.

Rys. 18. Wyniki siły osiowych w słupach układu stężeń

 

Podobnie jak w przypadku stężenia połaciowego, po zaprojektowaniu stężenia, należy przy wymiarowaniu słupa stężenia uwzględnić wartość siły ściskającej w tym słupie z analizy stężenia . Wartość tej dodatkowej siły w naszym zadaniu wynosi N_Ed,add = -8,3 kN.

4. Połaciowe stężenia poprzeczne wsporników

Warunki podparcia dla układów wydzielonych stężeń zależą od globalnej geometrii układu. W przykładzie z rozdziału 2 z  połaciowym stężeniem poprzecznym hali stalowej, stężeniu przypisano schemat belki swobodnie podpartej. Dla takiego schematu statycznego wyrażenie na imperfekcję łukową q_d podane jest bezpośrednio w normie [N2] ( Rys. 5.4). W przypadku innych schematów statycznych konieczne jest indywidualne ustalenie wyrażenia na zastępcze obciążenie q_d od imperfekcji łukowej.

 

Poniższy przykład przedstawia metodologię ustalania wartości q_d dla układu wspornikowego na przykładzie wiaty, jak na rysunku 19.

 

Rys. 19. Widok aksonometryczny wiaty wspornikowej

 

4.1 Analogia belkowa dla schematu wspornika

Schemat statyczny wydzielonego połaciowego stężenia poprzecznego powyższej konstrukcji pokazano poniżej

 

Rys. 20. Schemat statyczny wydzielonego układu stężenia połaciowego poprzecznego

 

Przedstawiony schemat statyczny stężenia w analogi belkowej odpowiada schematowi wspornika: 

 

Rys. 21. Analogia belkowa

 

Równoważne obciążenie imperfekcyjne wspornika

Przy wyznaczaniu wartości obciążenia q_d przyjęto zasadę, że obciążenie to ma generować taki sam moment zginający, co siła osiowa na ramieniu e₀:

 

 

(W.6)

 

skąd otrzymamy wzór na q_d

(W.7)

 

Odnosząc to wyrażenie do rozpatrywanego stężenia połaciowego, aby uzyskać wzór na zastępcze obciążenie imperfekcyjne należy dodać omawiane wcześniej przemieszczenie δ_q i uwzględnić liczbę elementów stężanych (porównaj ze wzorem W.2)

(W.8)

 

Wartość e₀ w tym przypadku (model ściskanego pręta wspornikowego ze wstępnym wygięciem) przez analogię do granicznych ugięć elementów wspornikowych w [N1] (NA. 22), gdzie L to podwójny wysięg wspornika, można przyjąć zgodnie ze wzorem

(W.9)

Przy określaniu wartości α_m, δ_q, oraz N_Ed,i należy postępować zgodnie z zasadami przedstawionymi w Obciążenia imperfekcyjne wydzielonych układów stężeń - Wprowadzenie. 

5. Połaciowe stężenia poprzeczne łuków - porównanie układów wydzielonych

Plik z zadaniem:

1. stezenie-luku-3D.axs
2. stezenie-luku-warianty.axs

Wymagana min. wersja AxisVM: X5 R4

Plik zawiera tylko model. Konieczne przeprowadzenie analizy w celu uzyskania wyników.

 

 

Rys. 22. Wiata z łukiem kratowym

 

Ustalenie układu wydzielonego w przypadku konstrukcji łukowych wymaga odrębnego komentarza, ponieważ przyjęcie poprawnego układu wydzielonego nie jest jednoznaczne. Problem przedstawiono na przykładzie wiaty z łukiem kratowym o rozpiętości 40,0m i wyniosłości łuku 12,0m.

 

5.1 Trzy warianty wyodrębnionych układów stężeń

Dla analizowanej konstrukcji przyjęto następujące trzy warianty układu wydzielonego stężenia połaciowego:

 

- zamodelowanie geometrii stężenia w postaci łuku, gdzie pasy górne kratownicy stanowią pasy stężenia 

 

Rys. 23. Wariant 1

 

-zamodelowanie geometrii stężenia w postaci łuku, gdzie pasy stężenia stanowione są przez „kompletną” kratownicę 

 

Rys. 24. Wariant 2

 

-zamodelowanie geometrii stężenia w postaci rozwinięcia stężenia do układu płaskiego, w którym pasy górne kratownicy stanowią pasy stężenia 

Rys. 25. Wariant 3

 

Poprawny schemat statyczny układu wydzielonego stężenia powinien charakteryzować się odpowiednią sztywnością. W tym celu porównano przemieszczenia poziome dla zaproponowanych wariantów układu wydzielonego stężenia (plik stezenie-luku-warianty.axs) pod obciążeniem równomiernie rozłożonym q = 5kN/m z przemieszczeniem poziomym odczytanym na modelu całej konstrukcji (plik stezenie-luku-3D.axs) obciążonej tak jak układy wydzielone. 

5.2 Wyniki

Uzyskane wyniki przemieszczeń oraz siły prętów krzyżowych stężeń

1. Wariant 1
   ey = 551,0mm;   Nmax = 70,9kN;   Nmin = -76,0kN 

1. Wariant 2
   ey = 16,6mm;   Nmax = 66,0kN;   Nmin = -71,3kN

1. Wariant 3
   ey = 15,2mm;   Nmax = 64,0kN;   Nmin = -68,7kN

1. Model całej konstrukcji (referencyjny)
   ey = 15,4mm;   Nmax = 67,4kN;   Nmin = -72,3kN

5.3 Wnioski

Przeprowadzona analiza wykazała, że układ wydzielony z wariantu 2 dokładnie odwzorowuje sztywność stężenia połaciowego. W przypadku układu wydzielonego dla wariantu 3 sztywność jest zaniżona, ale akceptowalna z inżynierskiego punktu widzenia. Wariant 1 stężenia wydzielonego daje niepoprawne wyniki i nie należy go stosować. 

Rys. 26. Deformacja układu stężenia w wariancie 1

 

 

Bibliografia

[N1] PN-EN 1993-1-1:2006, Projektowanie konstrukcji stalowych -- Część 1-1: Reguły ogólne i reguły dla budynków.

[N2] PN-B-03200:1990, Konstrukcje stalowe - Obliczenia statyczne i projektowanie

 

Copyright © 2021 by GammaCAD. Wszelkie prawa zastrzeżone.