Mimośrody w algorytmie projektowania wydzielonych elementów ściskanych

Mimośrody w algorytmie projektowania wydzielonych elementów ściskanych

Norma do projektowania konstrukcji żelbetowych PN-EN 1992-1-1:2008 wskazuje na konieczność uwzględnienia trzech mimośrodów w algorytmie wymiarowania wydzielonych elementów mimośrodowo ściskanych (jedno lub dwukierunkowo zginanych):
  1. mimośród statyczny es
  2. mimośród od imperfekcji geometrycznej ei
  3. mimośród drugiego rzędu e2

Algorytm do weryfikacji żelbetowych elementów ściskanych zaimplementowany jest w programie na zakładce Wymiarowanie - Żelbet > Słup żelbetowy.
Idea
Polecenie Słup żelbetowy może zostać użyte do zweryfikowania nośności żelbetowego elementu prętowego dowolnie usytuowanego na modelu (np. słup pochylony, belka).



Rys. 1. Sekcja z opcjami sterowania mimośrodami okna dialogowego parametrów do wymiarowania słupa żelbetowego

Poniżej zebrano najważniejsze informacje odnośnie wyznaczania mimośrodów w AxisVM przy wymiarowaniu metodą nominalnej krzywizny żelbetowych elementów ściskanych i zginanych. Jest to metoda dominująca w literaturze, dlatego na niej oparto rozważania, świadomie pomijając metodę nominalnej sztywności. Przeanalizowano wariantowo słup z następującymi założeniami (patrz Rys. 1):
  1. analiza wyboczenia w jednej płaszczyźnie, odpowiadająca płaszczyźnie zginania;
  2. układ nieprzechyłowy (przegub dołem-zamocowanie górą);
  3. wariantowe przebiegi momentów zginających i wykres siły normalnej (patrz Rys. 2)


    Rys. 2. Przyjęte wariantowe wykresy momentów zginających i siły normalnej 


1. Mimośród statyczny es

Mimośród statyczny es (określany również jako mimośród początkowy) jest funkcją MEd / NEd, gdzie MEd i NEd są siłami wewnętrznymi z analizy statycznej pierwszego rzędu. Siły te określane są automatycznie przez program dla wskazanego elementu, w jego punktach charakterystycznych (tj. węzłach końcowych oraz punktach występowania wartości ekstremalnych). Przy czym może to być zarówno cały element konstrukcyjny (np. słup) lub jego fragment. 


Rys. 3. Możliwe sposoby wskazania wymiarowanego elementu do wymiarowania (cały słup / odcinek słupa)


Notes
Jeśli podczas wymiarowania operujemy na fragmentach elementu konstrukcyjnego to należy pamiętać, aby w parametrach wymiarowania zaznaczyć opcję Zdefiniuj własną wysokość słupa i określić tę wartość w polu L [m]. Pozwoli to na  właściwe obliczenie imperfekcji geometrycznych i imperfekcji drugiego rzędu dla całego elementu wydzielonego w algorytmie wymiarowania.

Idea
Podział na fragmenty warto zastosować, jeżeli chcemy zróżnicować zbrojenie na długości słupa lub kiedy wykres siły osiowej jest istotnie zmienny skokowo.
 

➦ Przypadek A 

Słup dzielony jest na dwa przedziały, gdzie punkt podziału odpowiada ekstremum momentu przęsłowego My,Ed
  1. przedział A1.1 (od My,Ed = -75kNm do My,Ed = 57kNm), NEd,max = 274kN;
  2. przedział A1.2 (od My,Ed = 57kNm do My,Ed = 50kNm), NEd,max = 280kN.

Rys. 4. Rozkład momentu zginającego i siły podłużnej w przypadku A

Dla każdego przedziału program sprawdza wartość mimośrodu statycznego, przyjmując w uproszczeniu maksymalną wartość My,Ed i siły osiowej NEd,max
  1. esA1.1 = 75kNm/274kN = 0,273m
  2. esA1.2 = 57kNm/280kN = 0,204m
Do obliczeń w tym przypadku przyjmowany jest mimośród es = 0,273m, jako największa wartość z analizowanych przedziałów. Nie jest to jednak zasada obligatoryjna, ponieważ nie gwarantuje ona uzyskania maksymalnego wytężenia w elemencie dwukierunkowo zginanym (czytaj dalej).

W dalszej analizie słupa siła NEd odpowiada maksymalnej wartości z przedziału przyjętego do obliczeń, niezależnie od wartości tej siły w innych przedziałach analizowanego elementu. W rozważanym przypadku siła osiowa uwzględniana w obliczeniach będzie wynosiła 274kN, pomimo że w drugim przedziale wartość siły osiowej jest większa i wynosi 280kN.

➦ Przypadek B. 

Ekstremum przęsłowe momentu zginającego przypada na końcu słupa, dlatego nie ma potrzeby podziału słupa na więcej przedziałów. 

Rys. 5. Rozkład momentu zginającego i siły podłużnej w przypadku B


Wartość mimośrodu statycznego es wyznaczana jest jako iloraz maksymalnego momentu My,Ed i maksymalnej siły NEd tj. es = 100kNm/280kN = 0,357m. 

➦ Przypadek C. 

W tej sytuacji, podobnie jak w przypadku A, słup dzielony jest na dwa przedziały. Punkt podziału odpowiada ekstremum przęsłowemu momentu My,Ed: 
  1. przedział C1.1 (od My,Ed = -50kNm do My,Ed = 28kNm), NEd,max = 268kN ➠ es=0,200m;
  2. przedział C1.2 (od My,Ed = 28kNm do My,Ed = 0kNm), NEd,max = 280kN ➠ es=0,104m.

Rys. 6. Rozkład momentu zginającego i siły podłużnej w przypadku C


Odcinek C1.1 jest decydujący, jeżeli chodzi o wartość miarodajnego mimośrodu es.


➦ Przypadek D. 

Słup, w ramach działania modułu do wymiarowania, dzielony jest na dwa przedziały. Punkt podziału odpowiada ekstremum przęsłowemu momentu My,Ed: 
  1. przedział D1.1 (od My,Ed = -25kNm do My,Ed = 13kNm), NEd,max = 262kN ➠ es=0,100m;
  2. przedział D1.2 (od My,Ed = 13kNm do My,Ed = -50kNm), NEd,max = 280kN ➠ es=0,179m;.

Rys. 7. Rozkład momentu zginającego i siły podłużnej w przypadku D


Odcinek D1.2 w tym przypadku jest decydujący, jeżeli chodzi o wartość miarodajnego mimośrodu es.


Ważne

Na opisany powyżej sposób przyjmowania mimośrodu statycznego do wymiarowania słupa mogą mieć wpływ inne parametry:
  1. warunki brzegowe dla danego kierunku
    Definiuje się je poprzez wskazanie na rozwijanej liście odpowiadającej postaci wyboczenia. Należy zwrócić uwagę, że określają one jedocześnie czy dany element pracuje w układzie przechyłowym czy nieprzechyłowym

Rys. 8. Dostępne przy wymiarowaniu schematy pracy słupa

  1. Aktywowanie opcji Wylicz przyrost mimośrodu po kierunku ... dla jednego (patrz Rys. 1.) lub obu kierunków może prowadzić do przyjmowania różnych wartości mimośrodów dla pojedynczego kierunku.
Notes
Możliwa jest sytuacja, że przyjęta do wymiarowania przy jednokierunkowym zginaniu elementu dla danego kierunku  wartość mimośrodu es będzie się różnić od wartości przyjętej przy analizie dwukierunkowego zginania tego samego elementu.
W przypadku elementu dwukierunkowo zginanego istotne jest bowiem jednoczesne uwzględnienie obu kierunków. Do obliczeń przyjmowany i prezentowany jest w notce tylko przekrój z największym, całkowitym wykorzystaniem nośności. 


2. Mimośród ei jako efekt imperfekcji geometrycznej

W programie imperfekcję geometryczną wprowadzono do algorytmu wymiarowania słupa jako mimośród  ei, niezależnie od statycznej wyznaczalności układu/elementu wydzielonego. Mimośród przyjmuje wartość stałą dla nieprzechyłowej postaci wyboczenia (układ usztywniony), a wartość zmienną liniowo dla przechyłowej postaci wyboczenia (układ nieusztywniony), por. rys. 5.1a PN EN 1992-1-1.


Rys. 9. Sposób wyznaczania mimośrodu ei dla układu usztywnionego i nieusztywnionego


Mimośród wyliczany jest z poniższej zależności:

gdzie


Poprawne określenie wartości imperfekcji geometrycznej wymaga prawidłowego określenia długości wyboczeniowej słupa l0. Wartość ta, w module do wymiarowania słupa żelbetowego, domyślnie odnosi się do teoretycznej długości elementu wymiarowanego lt.

Info
W myśl normy PN-EN 1992-1-1 efekt imperfekcji geometrycznej powinien być uwzględniony na poziomie analizy statycznej. Sposób jego uwzględniania rozróżniony jest na wydzielone elementy statycznie wyznaczalne i statycznie niewyznaczalne. W przypadku elementów statycznie niewyznaczalnych, efekt imperfekcji geometrycznej należy uwzględnić poprzez przyłożenie zastępczej siły poziomej Hi. W przypadku elementów statycznie wyznaczalnych, alternatywnie dopuszczono wprowadzenie deformacji geometrii.


Notes
Istnieje możliwość uwzględnienia w programie imperfekcji geometrycznej na poziomie analizy statycznej. Polega to na zdefiniowaniu tej imperfekcji w jeden z poniższych sposobów:
  1. jako wstępnego przechyłu całej konstrukcji poprzez zdefiniowanie przypadku obciążenia Imperfekcja globalna

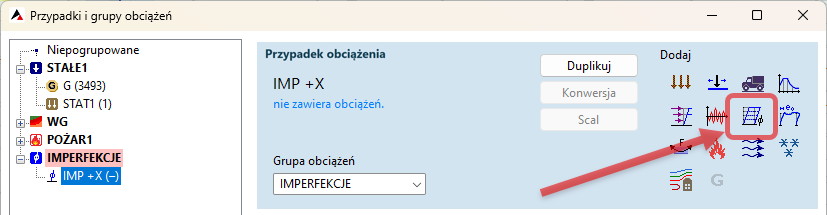
  2. jako układu zastępczych sił poziomych Hi będących funkcją kąta i i siły osiowej w słupie wg wzoru
     
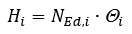
Jeżeli imperfekcja geometryczna została wprowadzona jednym z powyższych sposobów, to w oknie dialogowym z parametrami słupa (patrz Rys. 1.) należy zaznaczyć pole wyboru Tylko imperfekcje lokalne. Spowoduje to automatyczne potraktowanie słupa jako układu usztywnionego (nieprzechyłowego), dla którego określona zostanie dodatkowa imperfekcja geometryczna jak dla układu usztywnionego. Wynika to z bezpiecznego założenia przyjętego przez twórców programu, że oprócz globalnego przechyłu obiektu, pojedynczy słup może również ulec deformacji.

3. Mimośród wywołany efektami drugiego rzędu e2

Opcja Mimośród drugiego rzędu dla poszczególnych kierunków w oknie dialogowym parametrów (patrz Rys. 1.) steruje uwzględnieniem tego mimośrodu podczas weryfikacji elementu.
Efekty drugiego rzędu są pomijane:
  1. przy odznaczonej opcji Mimośród drugiego rzędu
  2. przy zaznaczonej opcji, gdy mamy do czynienia ze słupem krępym
W poprawnym określeniu wpływu efektów drugiego rzędu istotne jest przyjęcie właściwej krzywej wyboczeniowej odzwierciedlającej rzeczywiste zachowanie się słupa. Odbywa się to na podstawie odpowiedniego równania przypisanego do wskazanej przez użytkownika krzywizny, powiązanej ze sposobem zamocowania słupa. 

Notes
Krzywizna słupa do wyznaczania mimośrodów drugiego rzędu przyjmowana jest na podstawie wskazanego przez projektanta schematu pracy słupa w parametrach jego wymiarowania (patrz Rys. 8.), a nie na podstawie podpór zdefiniowanych w modelu globalnym.

Ponadto możliwe jest uwzględnienie w omawianym algorytmie mimośrodów drugiego rzędu na dwa sposoby:
  1. niezależnie po każdym kierunku,
  2. jako wypadkową z dwóch kierunków.
Rys. 10. Warianty uwzględniania mimośrodów drugiego rzędu

Generuje to, z racji braku w normie i literaturze precyzyjnych wskazówek, wiele pytań i wątpliwości.

W obu przypadkach mimośrody drugiego rzędu (e2y; e2z) są wyznaczane w ten sam sposób, co oznacza, że momenty zginające drugiego rzędu MyII i MzII również pozostają identyczne. Różnica między podejściami dotyczy sposobu „odmierzania” tych mimośrodów względem mimośrodu pierwszego rzędu e1 i powierzchni granicznej słupa wyznaczonej jako interakcja siły normalnej i momentów zginających. Mimośród pierwszego rzędu e1 jest sumą mimośrodu statycznego es oraz mimośrodu wynikającego z imperfekcji przechyłowej ei. Prosta łącząca środek ciężkości przekroju poprzecznego słupa z punktem mimośrodu e1 tworzy kąt a z osią poziomą przekroju poprzecznego słupa (osią y). Różnica między metodami wynika z interpretacji tych mimośrodów względem powierzchni granicznej określonej dla interakcji siły normalnej i momentów zginających.

W przypadku zastosowania pierwszej opcji (oznaczonej w tekście znakiem „+”), wartości ey i ez są odmierzane od położenia punktu e1 wzdłuż osi y’ (mimośród e2y) i z’ (mimośród e2z), które są osiami obróconymi o kąt α względem głównych osi przekroju poprzecznego słupa (patrz rysunek 11). 


Rys. 11. Graficzne przedstawienie mimośrodów drugiego rzędu wg pierwszej opcji

W drugim przypadku ((oznaczonej w tekście znakiem „x”) podejście jest odmienne: wyznaczany jest mimośród e2w, będący wypadkową mimośrodów e2y i e2z. Mimośród ten odkładany jest wzdłuż osi yII i zII, ustawionych pod kątem 45° względem głównych osi przekroju poprzecznego i zaczepionych w punkcie mimośrodu e1 (patrz rysunek 12).


Rys. 12. Graficzne przedstawienie mimośrodów drugiego rzędu wg drugiej opcji

Różnica w stopniu wykorzystania nośności słupa między obiema metodami wzrasta wraz ze zmniejszaniem się różnicy między momentami zginającymi w obu płaszczyznach (My; Mz). W przypadku zginania jednokierunkowego, wraz ze wzrostem udziału momentu zginającego względem siły normalnej, różnice w wynikach uzyskanych oboma powyższymi podejściami stopniowo zanikają, co ilustruje rysunek 13.

Rysunek 13. Zmiana stopnia wykorzystania słupa jednokierunkowo zginanego i ściskanego (+ odnosi się do wariantu pierwszego, x odnosi się do wariantu drugiego).


4. Mimośród miarodajny ed

Jest to mimośród uwzględniający mimośród statyczny, mimośród od imperfekcji geometrycznej i mimośród wywołany efektami drugiego rzędu. Wartość ta nie może być mniejsza od wartości minimalnej, określonej jako 

Notes
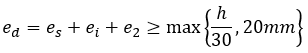
Wartość minimalna mimośrodu ed jest uwzględniana zawsze dla obu kierunków, nawet gdy opcja Wylicz przyrost mimośrodu po kierunku... została wyłączona dla jednego z nich.


    • Related Articles

    • Efektywna długość słupa żelbetowego

      Wymiarowanie wydzielonych ściskanych elementów żelbetowych metodami uproszczonymi (metoda nominalnej krzywizny i metoda nominalnej sztywności) wymaga określenia ich długości efektywnej l 0 . Definicja długości efektywnej l 0 znajdująca się w punkcie ...

    • Obciążenia imperfekcyjne wydzielonych układów stężeń

      1. Wprowadzenie Poprawnie zaprojektowany płaski układ prętowy jest samostateczny i geometrycznie niezmienny w „swojej płaszczyźnie”, (tj. płaszczyźnie -XZ-) będąc jednocześnie geometrycznie zmiennym w płaszczyźnie -YZ- (patrz rys. 1.)   Rys. 1. Widok ...

    • Obliczanie stopnia wykorzystania słupa żelbetowego

      Wybranie polecenie weryfikacja słupa żelbetowego uruchamia procedurę sprawdzenia nośności elementu żelbetowego poddanego dwukierunkowemu zginaniu z siłą podłużną. Procedurę weryfikacji żelbetowego elementu dwukierunkowo zginanego można uruchomić dla ...

    • Metoda ogólna wymiarowania elementów stalowych wg EC3

      zalecenia, zakres stosowania, algorytm, przykłady obliczeniowe 1. Kiedy należy stosować metodę ogólną? Norma PN-EN 1993-1-1:2006 umożliwia sprawdzenie stateczności z płaszczyzny elementów zginanych i ściskanych metodą ogólną (punkt 6.3.4) . ...

    • Wybór analizy globalnej dla stalowej konstrukcji ramowej

      Algorytm wyboru analizy statycznej oraz weryfikacji nośności ramowej konstrukcji stalowej w zależności od uzyskanego mnożnika krytycznego αcr. Dla różnych wariantów wybierano zawsze analizę możliwie najniższego rzędu., co nie wyklucza zastąpienia jej ...