Liniowa analiza wyboczeniowa - założenia i praktyczne zastosowania

Liniowa analiza wyboczeniowa - założenia i praktyczne zastosowania

Założenia LBA

Liniowa analiza wyboczeniowa (ang.linear buckling analysis - LBA ) pozwala na określenie postaci wyboczenia konstrukcji i odpowiadających im wartości własnych .

Założenia liniowej analizy wyboczeniowej są następujące:
  1. obciążenie jest jednoparametryczne,
    czyli określone jako Fcr = αcr * F0 , gdzie αcr   jest parametrem obciążenia (mnożnikiem) a  F0   jest obciążeniem pierwotnym (przyłożonym),
  2. obciążenie jest zachowawcze
    tj. nie „podąża” za deformującą się konstrukcją (punkt i kierunek obciążenia nie zmienia się),
  3. analiza nie uwzględnia nieliniowości geometrycznych i fizycznych
    (np. wiotkich stężeń zamodelowanych jako pręty kratowe pracujące tylko na rozciąganie).

Podstawowe pojęcia

Postacie wyboczenia przedstawiają bezwymiarową (o nieokreślonej wielkości) deformację konstrukcji przy wyboczeniu (utracie stateczności).
Wartości własne (zwane również mnożnikami obciążenia krytycznego αcr ) określają wielokrotność obciążenia, przy którym nastąpi dana postać utraty stateczności.
Obciążenie krytyczne Fcr   to obciążenie, po osiągnięciu którego następuje wyboczenie. Definiujemy je jako iloczyn wartości własnej i aktualnego obciążenia Fcr = αcr * F0

Interpretacja wielkości mnożnika krytycznego αcr 

W kontekście przedstawionej definicji obciążenia krytycznego możemy wyszczególnić ogólne zakresy mnożnika krytycznego: 
  1. αcr < 1,0
    przyłożone obciążenie jest większe od obciążenia krytycznego, co w praktyce oznacza, że warunki brzegowe dla konstrukcji zostały błędnie przyjęte lub jej elementy są zbyt smukłe, w wyniku czego już od części projektowanego obciążenia traci ona swoją stateczność
  2. αcr = 1,0
    moment przejścia (przyłożone obciążenie jest równe obciążeniu krytycznemu), w którym konstrukcja zaczyna „pracować” w nowej formie (np. ściskanie osiowe przechodzi w ściskanie mimośrodowe)
  3. αcr > 1,0
    przyłożone obciążenie jest mniejsze od obciążenia krytycznego, co oznacza, że nie wystąpi utrata stateczności pod warunkiem niewystąpienia imperfekcji geometrycznych i materiałowych oraz innych nieliniowości fizycznych

Zastosowanie analizy wyboczeniowej

Liniowa analiza wyboczeniowa wykorzystywana jest zarówno dla konstrukcji prętowych i powłokowych, co pozwala wykorzystać ją w rozwiązywaniu wielu problemów inżynierskich. Jest ona obok liniowej analizy statycznej jednym z pierwszych sprawdzeń poprawności modelu oraz przyjętych założeń. W zależności od typu zastosowanych na modelu elementów, uzyskamy różne zakresy odpowiedzi konstrukcji. W tabeli poniżej zestawiono wspomniane zakresy.

Tabela 1. Rodzaje postaci wyboczenia a typ elementu MES
POSTAĆ WYBOCZENIA

 Pręt 6 DoF

Pręt 7 DoF 

Powłoka 

 lokalna

-

-

+

 

  globalna

 

giętna

+

+

+

 skrętna

-

+

+

 giętno-skrętna

-

+

+

Zastosowanie liniowej analizy wyboczeniowej w odniesieniu do prętowych konstrukcji inżynierskich (drewniane, żelbetowe, stalowe) pozwala na:
  1. sprawdzenie poprawności zamodelowanej konstrukcji pod kątem zadanych warunków brzegowych,
  2. określenie mnożnika obciążenia krytycznego elementów lub całej konstrukcji i w konsekwencji nośności krytycznej elementu lub całej konstrukcji (patrz przykład poniżej)
  3. określenie wrażliwość konstrukcji na efekty drugiego rzędu (więcej informacji tutaj),
  4. znalezienie kształtu imperfekcji przechyłowych i łukowych, które następnie mogą być zaimplementowane w modelu statycznym,
  5. wyznaczenie długości wyboczeniowej elementów narażonych na globalną formę utraty stateczności.

Przykłady

1. Element 6 DoF

Analiza wyboczeniowa elementów z węzłowymi 6 stopniami ( 6 DoF) pozwala na określanie tylko giętnej postaci wyboczenia (patrz tabela 1). W oparciu o jej wyniki możemy określić nośność krytyczną pręta poddanego ściskaniu.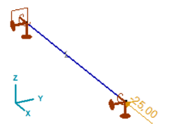

Rys. 1. Pręt osiowo ściskany siłą N Ed  = 25kN, przekrój IPE 120, L=4 m.

Wyboczenie z płaszczyzny
Po wykonaniu analizy wyboczeniowej uzyskujemy αcr   = 1,434 (pierwsza postać wyboczenia w płaszczyźnie x-y jest również pierwszą postacią modelu).  Co za tym idzie, nośność krytyczna pręta przy ściskaniu wynosi Ncr,xy  = αcr  *NEd  = 1,434 * 25kN = 35,85kN

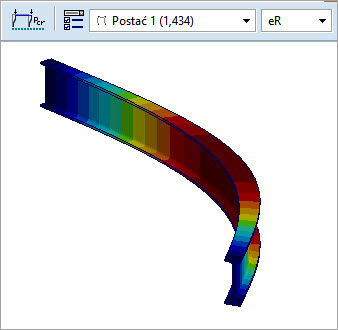Rys. 2. Pierwsza postać wyboczenia z płaszczyzny

Analityczne sprawdzenie wg wzoru Eulera



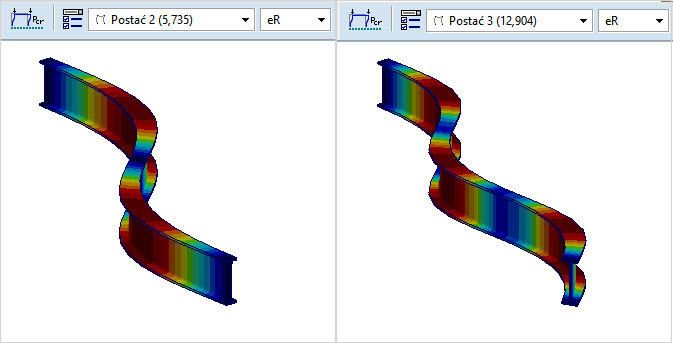
Rys. 3. Druga i trzecia postać wyboczenia z płaszczyzny (nieistotna)

Wyboczenie w płaszczyźnie
αcr = 16,467 to pierwsza postać wyboczenia w płaszczyźnie x-z i zarazem czwarta postać modelu. Nośność krytyczna  Ncr,xz  =αcr  *NEd   = 16,467 * 25kN = 411,68kN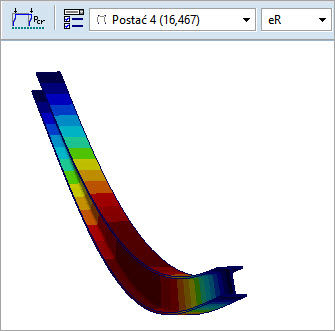 

Rys. 4. Pierwsza postać wyboczenia w płaszczyźnie

Sprawdzenie analityczne


Wyniki referencyjne z modelu powłokowego
αcr  =1,429 - pierwsza postać wyboczenia w płaszczyźnie x-y 
Ncr,xy  = αcr *NEd  =1,429 * 25kN = 35,7kN
αcr   = 16,092 - pierwsza postać wyboczenia w płaszczyźnie x-z 
Ncr,xz = αcr *NEd  = 16,092 * 25kN = 402,30kN

2. Element 7 DoF

Analiza wyboczeniowa elementów z węzłowymi 7 stopniami (7 DoF) pozwala na określenie giętno-skrętnej postaci wyboczenia  (patrz tabela 1) . W związku z tym, opierając się na wyniku dla odpowiedniej postaci możemy określić sprężysty moment krytyczny (Mcr ) pręta poddanego czystemu zginaniu.


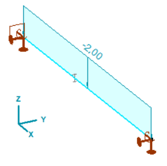
Rys. 5.  Pręt zginany o przekroju IPE 120, q=2kN/m w środku ciężkości przekroju, L = 4m, M Ed,max  =400kNcm

Dla pręta 6 DoF poddanego czystemu zginaniu (powyższy przykład) nie jest możliwe uzyskanie jakichkolwiek wyników z analizy wyboczeniowej ze względu na brak jego ściskania.

Wyboczenie giętno-skrętne
αcr  =2,069 uzyskujemy dla pierwszej giętno-skrętnej postaci wyboczenia, co odpowiada pierwszej postaci  modelu.
Mcr  = αcr *MEd  = 2,069 * 400kNcm = 827,6kNcm


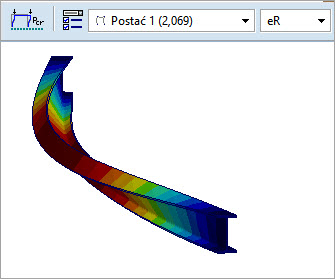
Rys. 6. Pierwsza postać wyboczenia giętno-skrętnego

Sprawdzenie analityczne


Wyniki referencyjne z modelu powłokowego
αcr  = 1,844 - pierwsza giętno-skrętna postać wyboczenia
Mcr  = αcr *MEd  = 1,844 * 400kNcm = 737,6kNcm


    • Related Articles

    • Współpraca belki stalowej z blachą trapezową, płytą warstwową lub żelbetową

      1. Informacje wstępne Połączenie belki stalowej z konstrukcyjnym elementem powierzchniowym może zapewnić jej dodatkowe podparcie ciągłe, a tym samym zabezpieczyć całkowicie lub częściowo przed utratą płaskiej postaci zginania, czyli przed ...

    • Efektywna długość słupa żelbetowego

      Wymiarowanie wydzielonych ściskanych elementów żelbetowych metodami uproszczonymi (metoda nominalnej krzywizny i metoda nominalnej sztywności) wymaga określenia ich długości efektywnej l 0 . Definicja długości efektywnej l 0 znajdująca się w punkcie ...

    • Wyznaczenie wielkości strzałki wygięcia i przechyłu dla imperfekcji

      Imperfekcje geometryczne konstrukcji mogą zostać zdefiniowane na modelu w sposób bezpośredni lub w niektórych przypadkach uwzględnione na etapie wymiarowania elementu w sposób pośredni (patrz  Wybór analizy globalnej dla stalowej konstrukcji ...

    • Wymiarowanie rygla ramy portalowej z dachem dwuspadowym

      1. Podparcie rygla Podczas wymiarowania rygla ramy portalowej z dachem dwuspadowym często przyjmuje się bez głębszej analizy, że podparcie rygla w płaszczyźnie układu stanowią słupy. Przyjęte podparcie w płaszczyźnie układu wpływa bezpośrednio na ...

    • Wybór analizy globalnej dla stalowej konstrukcji ramowej

      Algorytm wyboru analizy statycznej oraz weryfikacji nośności ramowej konstrukcji stalowej w zależności od uzyskanego mnożnika krytycznego αcr. Dla różnych wariantów wybierano zawsze analizę możliwie najniższego rzędu., co nie wyklucza zastąpienia jej ...